Generalized dessins — Part 1: the definition

Grothendieck’s initial wonder for the action of \(G_{\Q}=\Gal(\Qbar\mid\Q)\) on étale covers of the projective line minus three points comes from the “childlike” combinatorial description offered by the theory of dessins d’enfants. This theory, although elementary, is rich enough to be acted upon faithfully by \(G_{\Q}\), as a consequence of Belyĭ’s theorem. In this blog post, I suggest a generalization of this elementary description for covers of the line branched at more than three points (dessins d’ados?).

We fix an integer \(n \geq 2\), which serves as the number of colors used for the vertices (spoiler alert: this will be the number of branch points minus one, so \(n=2\) is the case of dessins d’enfants). We use the following definition of a cyclical order (always on a finite set):

Definition (cyclical order): A cyclical order on a finite set \(X\) is a permutation of \(X\) consisting of a single cycle of length \(\card{X}\). If \(x \in X\), we call successor of \(x\) in the cyclical order the image of \(x\) by the corresponding permutation.

the category of dessins

Definition (\(n\)-dessin): An \(n\)-dessin consists of the following data:

• For each color \(i \in \{1,\ldots,n\}\), a finite set \(V_i\), whose elements are called vertices of color \(i\).
• A finite set \(E\), whose elements are called hyperedges, and \(n\) surjective maps \(s_i : E \to V_i\). If \(e \in E\) is a hyperedge, \(s_i(e)\) is called the vertex of \(e\) of color \(i\).
• For each color \(i \in \{1,\ldots,n\}\) and each vertex \(v \in V_i\), a cyclical order on the subset \(s_i^{-1}(v)\) of \(E\) (consisting of hyperedges whose vertex of color \(i\) is \(v\)).

The case \(n=2\) corresponds to dessins d’enfants, for which hyperedges are simply edges.

We now give an example of a \(3\)-dessin. This will be our go-to example to illustrate all later notions:

Example: We denote by \(\D_0\) the \(3\)-dessin defined by the following data:

• \(V_1 = \{r, r'\}\), \(V_2 = \{g, g'\}\), \(V_3 = \{b, b'\}\), \(E = \{1, 2, 3, 4\}\).
• The maps \(s_i\) are given by the following table:

• The cyclical order on hyperedges having \(g\) as their vertex of color \(2\) is \((1,2,3)\). All other cyclical orders are forced because they are on sets of size two or one.

We now define morphisms between dessins:

Definition (morphism of dessins): Let \(\D=(V_i, E, s_i)\) and \(\D'=(V'_i, E', s'_i)\) be two \(n\)-dessins. A morphism \(D' \to \D\) is a collection of maps \(\Sigma_i : V'_i \to V_i\) and \(\Phi : E' \to E\) such that:

• for every color \(i \in \{1,\ldots,n\}\), we have \(\Sigma_i \circ s'_i = s_i \circ \Phi\), i.e. the following diagram commutes:

  \[\begin{matrix} E' & \overset{s'_i}{\to} & V'_i \\ {\scriptsize\Phi} \downarrow & & \downarrow{\scriptsize\Sigma_i} \\ E & \underset{s_i}{\to} & V_i \end{matrix}\]

• for every vertex \(v \in V'_i\) and for every hyperedge \(e \in (s'_i)^{-1}(x)\), the map \(\Phi\) maps the successor of \(e\) in the cyclical order on \((s'_i)^{-1}(v)\) to the successor of \(\Phi(e)\) in the cyclical order on \(s_i^{-1}(\Sigma_i(v))\). This implies that \((s'_i)^{-1}(v)\) is obtained by “assembling” a certain (integer) number of copies of \(s_i^{-1}(\Sigma_i(v))\), one after another.

When \(\alpha\) is a morphism of dessins \(\D' \to \D\) and \(v\) is a vertex (resp. \(e\) is a hyperedge) of \(\D'\), we write \(\alpha(v)\) (resp. \(\alpha(e)\)) instead of \(\Sigma_i(v)\) (resp. \(\Phi(e)\)).

These two notions define a category \(\Dess_n\) of \(n\)-dessins.

Definition (degree of a dessin): The degree of an \(n\)-dessin \(\D\) is the number of hyperedges \(\card{E}\).

Definition (degree of a vertex): The degree \(\deg(v)\) of a vertex \(v \in V_i\) is the number of hyperedges whose vertex of color \(i\) is \(v\). In other words, \(\deg(v) = \card{s_i^{-1}(v)}\).

Proposition: Let \(\alpha : \D \to \D'\) be a morphism of dessins and \(v\) be a vertex of \(\D\). Then, \(\deg(v)\) is a multiple of \(\deg(\alpha(v))\).

Definition (index of a color): The index of the color \(i\) in an \(n\)-dessin \(\D\) is the nonnegative integer:

drawing a dessin

To draw a dessin, we adopt the following conventions:

• If \(n=2\), vertices of \(V_1\) are represented by black disks, and vertices of \(V_2\) by white disks. If \(n \geq 3\), the colors used for vertices are, in that order: red, green, blue, brown.

• The interior of hyperedges is always colored yellow. If \(n=2\), (hyper)edges are either represented as standard, one-dimensional edges, or as “digons”:

  

  If \(n \geq 3\), hyperedges are drawn as \(n\)-gons whose edges are not necessarily straight, or equivalently as embeddings of the disk with \(n\) marked points on its boundary, having a single marked point for each color \(i\) (given by the map \(s_i\)). Importantly, we require that the colors of the marked points appear in the cyclical order \((1, 2, \ldots, n)\) when the boundary of the \(n\)-gon/disk is travelled counterclockwise.

• Let \(v\) be a vertex. The cyclical order on hyperedges having \(v\) as a vertex is the order in which these hyperedges appear when one rotates counterclockwise around the vertex \(v\).

These constraints define a notion of “good embeddings” of a dessin on a compact oriented surface. If one moreover requires that the complement of the image of this embedding be a disjoint union of disks (to avoid “unnecessary genus”), these constraints rigidify the surface and the embedding if we identify two embeddings which are related by a direct homeomorphism between the surfaces. In other words, dessins (which we have defined abstractly) also admit an equivalent (slightly more geometrical) definition as embeddings of \(n\)-partite hypergraphs into compact oriented surfaces satisfying the conditions above, identified each time they are related by a direct homeomorphism of the surface.

Because of these conventions, dessins can not always be drawn on paper (or, in this case, on your computer screen): because of this, we will have to draw some overlaps (an hyperedge passes “above” another), in which case we use the same conventions as when drawings e.g. knots or braids.

Example: We draw the dessin \(\D_0\) defined earlier:

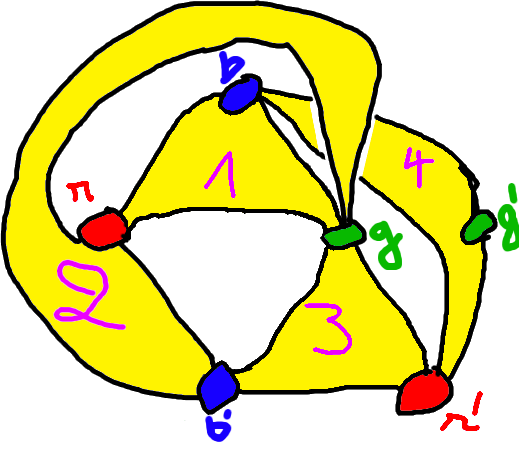
As you can see, there is an (unavoidable) overlap between hyperedges \(2\) and \(4\). This illustrates the fact that this dessin can be embedded on the surface of a torus (you can imagine drawing this picture on the surface of a coffee cup: hyperedge \(2\) is drawn on the handle, hyperedge is drawn “below” the handle), but not on a genus \(0\) surface like a sheet of paper or a computer screen…

monodromy

Definition (monodromy elements): Let \(\D = (V_i, E, s_i)\) be an \(n\)-dessin. For every integer \(i \in \{1, \ldots, n\}\), the \(i\)-th monodromy element of \(\D\) is the permutation \(\sigma_i \in \Sym_E\) of the hyperedges defined in the following way: \(\sigma_i\) is the product of as many cycles with disjoint supports as there are vertices in \(V_i\), and for each vertex \(v \in V_i\), the corresponding cycle is the permutation of \(s_i^{-1}(v)\) associated to the cyclical order.

The degree of a vertex \(v \in V_i\) is equal to the size of the cycle of \(\sigma_i\) associated to \(v\). The order of \(\sigma_i\) is equal to the least common multiples of all degrees of vertices of color \(i\).

Definition (monodromy group): Let \(\D = (V_i, E, s_i)\) be an \(n\)-dessin. The monodromy group \(\gen{\D}\) of \(\D\) is the subgroup of \(\Sym_E\) generated by the monodromy elements \(\sigma_1, \ldots, \sigma_n\).

We also define the \((n+1)\)-th monodromy element \(\sigma_{n+1}\) as the element \((\sigma_1 \cdots \sigma_n)^{-1} \in \gen{\D}\). This way, we have the useful identity:

Example: The \(3\)-dessin \(\D_0\) described earlier has monodromy elements \(\sigma_1 = (12)(34)\), \(\sigma_2 = (132)\), \(\sigma_3 = (14)(23)\), \(\sigma_4 = (134)\), and its monodromy group \(\gen{\D_0}\) is the alternating group \(\mathfrak{A}_4\).

The definition of morphisms of dessins directly implies:

Lemma: Let \(\alpha : \D \to \D'\) be a morphism of \(n\)-dessins, \(i \in \{1,\ldots,n\}\) be a color, and \(e \in E\) be a hyperedge of \(\D\). Then \(\alpha(\sigma_i.e) = \sigma_i.\alpha(e)\). In particular, if \(\D\) is a dessin, the action of the monodromy group \(\gen{\D}\) on hyperedges commutes with the action of the automorphism group of \(\D\) on hyperedges.

dessins and branched covers of the line

configurations and bouquets

Denote by \(\PConf_{n+2}(\C)\) the set of ordered lists of \(n+2\) distinct points of the Riemann sphere \(\P^1(\C)\), which we call configurations. Fix a configuration \((t_0, t_1, \ldots, t_n, t_{n+1}) \in \PConf_{n+2}(\C)\). Let \(X\) denote the pointed topological space \((\P^1(\C) \setminus \{t_1, \ldots, t_{n+1}\}, t_0)\).

Definition (bouquet): A bouquet of \(X\) is a set of loops \(\gamma_1, \ldots, \gamma_{n+1}\) based at \(t_0\) satisfying the following conditions:

• for each \(i \in \{1, \ldots, n+1\}\), \(\gamma_i\) is homotopic to the positively oriented generator of \(\pi_1(\P^1(\C) \setminus \{t_i\}, t_0) \simeq \Z\) when the points \(t_j, j\neq i\) are put back in,
• for each \(i \in \{1, \ldots, n+1\}\), \(\gamma_i\) is homotopic to the trivial loop \(1 \in \pi_1(\P^1(\C) \setminus \{t_j, j \neq i\}, t_0)\) when the point \(t_i\) is put back in,
• the trajectories of the loops \(\gamma_i\) and \(\gamma_j\) do not intersect (except at the point \(t_0\) at the beginning and end) when \(i \neq j\),
• the cyclical order in which one meets these loops when one rotates positively around the point \(t_0\) is \((\gamma_1, \ldots, \gamma_{n+1})\).

Under these conditions, the loops \(\gamma_1, \ldots, \gamma_n\) generate \(\pi_1(X)\) freely, and these loops satisfy the relation \(\gamma_1 \cdots \gamma_{n+1} = 1\). We denote the set of bouquets of \(X\) by \(\Isomp(\pi_1(X), F_n)\).

dessins and covers

Fix a bouquet \(\gamma_1, \ldots, \gamma_{n+1}\), which we see as a (very particular) isomorphism of groups \(\gamma : \pi_1(X) \to F_n\). This isomorphism induces an equivalence of categories between the category of finite étale covers of \(X\), classically equivalent to the category of finite \(\pi_1(X)\)-sets, and that of finite \(F_n\)-sets (finite sets equipped with an action of the free group on \(n\)-letters).

Now, if \(\D\) is a dessin, the morphism \(\varphi : F_n \to \Sym_E\) which maps the \(i\)-th letter to the \(i\)-th monodromy element of \(\D\) defines a \(\pi_1(X)\)-set. This construction actually defines a functor \(\Dess_n \to F_n\text{-sets}\) (exercise: define the image of morphisms of dessins). In the other direction, if one has an \(F_n\)-sets incarnated by a group morphism \(F_n \to \Sym_E\) for some finite set \(E\), we can define an \(n\)-dessin in the following way:

• the set \(V_i\) of vertices of color \(i\) is the set of cycles (including fixed points) in the image in \(\Sym_E\) of the \(i\)-th letter (generator of \(F_n\)),
• the cyclical order on hyperedges (elements of \(E\)) whose vertex of color \(i\) are a given \(v \in V_i\) is given by the cycle \(v\) itself.

In other words, an \(n\)-dessin whose set of hyperedges is \(E\) is characterized by the \(n\)-tuple \((\sigma_1, \ldots, \sigma_n)\) of elements of \(\Sym_E\) (image of the letters under the morphism \(\varphi\)), or equivalently by the \((n+1)\)-tuple \((\sigma_1,\ldots,\sigma_n,\sigma_{n+1})\) of elements satisfying the additional property that \(\sigma_1 \cdots \sigma_{n+1} = 1\).

These two inverse constructions define an equivalence of categories between \(n\)-dessins and \(F_n\)-sets. This means that for each choice of configuration and bouquet, we have:

Theorem: The category \(\Dess_n\) of \(n\)-dessins is equivalent to the category of finite unramified covers of the Riemann sphere punctured at \(n+1\) given points.

By Riemann’s existence theorem, the latter category is itself equivalent to the category of dominant and generically étale finite maps from a smooth curve to \(\P^1_{\C}\), unramified outside the points \(t_1, \ldots, t_{n+1}\), or to the category of field extensions of \(\C(T)\) which are unramified outside \(n+1\) places.

The degree of the cover corresponding to a given dessin is the number of hyperedges of that dessin.

graphical interpretation

The relation between \(n\)-dessins and covers of the \(n+1\)-punctured Riemann sphere can be interpreted graphically. To this end, one draws a yellow disk on the Riemann sphere, not containing the point \(t_{n+1}\), on the boundary of which one marks \(n\) points \(t_1, \ldots, t_n\), appearing in this order (or a circular permutation thereof) when one travels counterclockwise along the boundary.

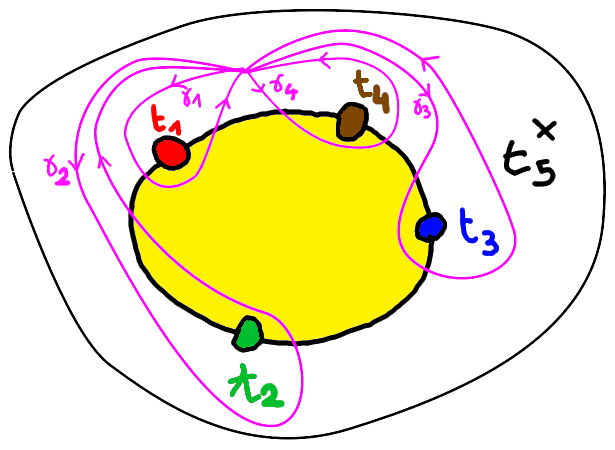
Consider a finite cover of \(\P^1(\C)\), unramified outside \(t_1, \ldots, t_{n+1}\). The hyperedges of the corresponding \(n\)-dessin are the inverse images of the yellow disk. The red vertices are the inverse images of the point \(t_1\), etc. The cyclical order on the hyperedges with a given vertex is seen in the following way: when one keep rotating counterclockwise around the green point \(t_2\) (following the loop \(\gamma_2\) multiple times), one crosses the yellow disk at each new loop. Look at the trajectory of a lift of these rotations through the covering map: you see a rotating path around a green vertex \(v\), which intersects different yellow disks (having \(v\) as their green vertex) until it eventually loops. The order of appearances of these yellow disks during the full loop is the cyclical order on the set of hyperedges whose green vertex is \(v\).

an off-topic question

The following fact was told to me by Olivier Benoist:

Theorem: A curve that has a finite morphism to \(\P^1_{\C}\), generically étale and unramified outside four points, is necessarily defined over a finite extension of \(\Q(T)\).

This is a generalization of the “easy part” of Belyĭ’s theorem. For the proof, we denote by \(\Qbar_T\) the algebraic closure of \(\Q(T)\) (MathJax messes the formatting of \overline{\Q(T)} for some reason)

Proof: Using a homography, one can assume that the four branch points are \(0,1,\infty, \lambda\) for some \(\lambda\) (deduced from the cross-ratio of the original four branch points).

• If \(\lambda\) is algebraic, extension of scalars induces an isomorphism:

  \[\piet\left(\P^1_{\C}\setminus\{0,1,\infty,\lambda\}\right) \simeq \piet\left(\P^1_{\Qbar}\setminus\{0,1,\infty,\lambda\}\right).\]

  So our cover, and hence the curve, is defined over a number field.

• If \(\lambda\) is transcendental, choose an embedding of \(\Qbar_T\) into \(\C\) which maps \(T\) to \(\lambda\). As before, extension of scalars (from \(\Qbar_T\) to \(\C\)) induces an isomorphism:

  \[\piet(\P^1_{\C}\setminus\{0,1,\infty,\lambda\}) \simeq \piet\left(\P^1_{\Qbar_T}\setminus\{0,1,\infty,T\}\right).\]

  Hence our cover comes from a cover of \(\P^1_{\Qbar_T}\) via extension of scalars, and hence the curve is defined over \(\Qbar_T\). ■

More generally, the transcendance degree (over \(\Q\)) of the field of definition of a cover of \(\P^1_{\C}\) is at most equal to the transcendance degree of the \(\Q\)-algebra generated by all cross-ratios between the branch points.

Question: Is the theorem above an equivalence? i.e., can we generalize Belyĭ’s theorem to more general situations in this way?

My guess is that the answer is no.

In the next blog post, we will discuss the notions of connectedness and regularity of a dessin. Our ultimate goal is to describe “as combinatorially as possible” the action(s) of the absolute Galois group on these generalized dessins.