Generalized dessins — Part 2: connected/regular/clean dessins

Created in August 08, 2023

2023   ·   dessins-saga

$$\require{color}$$ $$\newcommand{\Q}{\mathbb{Q}}$$ $$\newcommand{\C}{\mathbb{C}}$$ $$\newcommand{\Z}{\mathbb{Z}}$$ $$\newcommand{\P}{\mathbb{P}}$$ $$\newcommand{\tbar}{\underline{t}}$$ $$\newcommand{\Qbar}{\overline{\Q}}$$ $$\newcommand{\Gal}{\mathrm{Gal}}$$ $$\newcommand{\Sym}{\mathfrak{S}}$$ $$\newcommand{\card}[1]{\left| #1 \right|}$$ $$\newcommand{\gen}[1]{\left\langle #1 \right\rangle}$$ $$\newcommand{\todo}[1]{\color{red}\textbf{[TODO] #1}}$$ $$\newcommand{\D}{\mathcal{D}}$$ $$\newcommand{\Dess}{\mathfrak{Dessins}}$$ $$\newcommand{\PConf}{\mathrm{PConf}}$$ $$\newcommand{\Isomp}{\mathrm{Isom}^+}$$ $$\newcommand{\piet}{\pi_1^{\text{ét}}}$$
Quick navigation: Part 1 — Part 2 (current) — Part 3 — to be continued…

This post assumes you have read Part 1!

In this blog post, we define and study the notions of connected, regular and clean dessins (dessins were introduced in the previous post). This post is less “conceptual” than the previous one and mostly consists of technicalities.

In proofs, we use the following property: two hyperedges \(e, e' \in E\) share the same vertex of color \(i \in \{1,\ldots,n\}\) if and only if there exists an integer \(k\) such that \(e' = \sigma_i^k.e\).

connected dessins

Definition (connected): A dessin \((V_i, E, s_i)\) is connected if for all hyperedges \(e, e' \in E\) there exist hyperedges \(e = e_0, e_1, \ldots, e_r = e'\) and colors \(i_1, \ldots, i_r \in \{1,\ldots,n\}\) such that \(s_{i_k}(e_{k-1}) = s_{i_k}(e_k)\).

Notice that \(e_k = \sigma_{i_k}^{l_k}.e_{k-1}\) for some integer \(l_k\), and thus \(e' = \sigma_{i_r}^{l_r} \cdots \sigma_{i_1}^{l_1} . e\). This leads to the following proposition:

Proposition: A dessin is connected if and only if its monodromy group acts transitively on the set of its hyperedges.

Since transitive \(F_n\)-sets correspond to connected covers of the \(n\)-punctured Riemann sphere, we have:

Corollary: A dessin is connected if and only if the corresponding cover is connected. (for any choice of configuration/bouquet)

Proposition: The automorphism group of a connected dessin acts freely on the set of its hyperedges.

Proof: Let \(\alpha\) be an automorphism which fixes a hyperedge \(e \in E\). Our goal is to show that \(\alpha\) is the identity morphism. Consider a hyperedge \(e' \in E\). By connexity, there is an element \(g\) of the monodromy group such that \(e' = g.e\). We have \(\alpha(e') = \alpha(g.e) = g.\alpha(e) = g.e = e'\). So \(\alpha\) fixes every hyperedge. Since every vertex \(v \in V_i\) can be retrieved as the vertex of the vertex of color \(i\) of some hyperedge and morphisms preserve colors, \(\alpha\) also fixes every vertex. We have showed that \(\alpha\) is the trivial automorphism. ■

regular dessins

The notion of regularity for graphs is a model of homogeneity, of sameness of every part, i.e. it tends to ensure the existence of many automorphisms. We define a similar notion for dessins:

Definition: A dessin is regular if its automorphism group acts transitively on the set of its hyperedges.

Typically, the degree of a vertex of a regular dessin depends only on its color.

properties of regular dessins

In terms of covers, regularity is a well-known property:

Proposition: A dessin is regular if and only if the corresponding cover is Galois. (for any choice of configuration/bouquet)

Proposition: The automorphism group of a connected regular dessin is isomorphic to its monodromy group.

Proof: For the whole proof, fix a hyperedge \(e \in E\). Let \(g\) be an element of the monodromy group, which takes \(e\) to the hyperedge \(g.e\). The action of the automorphism group on hyperedges is free (by a previous property) and transitive (by regularity), so there is a unique automorphism \(\alpha_e(g)\) satisfying \(\alpha_e(g)(g.e) = e\).

We show that the map \(\alpha_e : g \mapsto \alpha_e(g)\) is a group isomorphism:

  • \(\alpha_e\) is a group morphism: Let \(g, g'\) be elements of the monodromy group. Then the automorphism \(\alpha_e(g) \alpha_e(g')\) satisfies:

    \[\alpha_e(g) \alpha_e(g') (gg'.e) = \alpha_e(g) (g. \alpha_e(g') (g'.e)) = \alpha_e(g) (g.e) = e\]

    By construction, this means that \(\alpha_e(g) \alpha_e(g') = \alpha_e(gg')\).

  • \(\alpha_e\) is injective: Assume \(\alpha_e(g) = 1\). By definition, we have \(g.e = e\). Let \(e' \in E\). By regularity, there is an automorphism \(\beta\) such that \(\beta(e) = e'\). We have \(g.e' = g.\beta(e) = \beta(g.e) = \beta(e) = e'\). So \(g \in \Sym_E\) is the trivial permutation.
  • \(\alpha_e\) is surjective: Let \(\beta\) be an automorphism. By connectedness, there is an element \(g\) of the monodromy group such that \(g.\beta(e) = e\). We then have \(\beta(g.e)=e\) and thus \(\beta = \alpha_e(g)\) by definition.

■

Proposition: A connected dessin is regular if and only if its monodromy group acts freely on the set of its hyperedges.

Proof: As we have seen, the monodromy group of a regular connected dessin is isomorphic to its automorphism group, and thus acts freely on hyperedges.

Conversely, assume the action of the monodromy group on the set of its hyperedges is free (recall that it is transitive by connectedness). Let \(e \in E\) be an hyperedge. To every automorphism \(\alpha\), one associates the unique element \(g_e(\alpha)\) of the monodromy group satisfying \(g_e(\alpha).e = \alpha^{-1}(e)\).

  • \(g_e\) is a group morphism: Let \(\alpha, \alpha'\) be automorphisms. Then:

    \[g_e(\alpha).g_e(\alpha').e = g_e(\alpha).(\alpha')^{-1}(e) = (\alpha')^{-1}(g_e(\alpha).e) = (\alpha')^{-1}(\alpha^{-1}(e)) = (\alpha \alpha')^{-1}(e)\]

    and thus \(g_e(\alpha \alpha') = g_e(\alpha) g_e(\alpha')\) by freeness.

  • \(g_e\) is injective: Assume \(g_e(\alpha)=1\), i.e. \(\alpha(e) = e\). By connectedness, for every hyperedge \(e' \in E\) there is an element \(g\) of the monodromy group such that \(e'=g.e\), and then \(\alpha(e')=\alpha(g.e)=g.\alpha(e)=g.e=e'\). So \(\alpha\) fixes every hyperedge, and is therefore the trivial automorphism.
  • \(g_e\) is surjective: Let \(g\) be an element of the monodromy group. We define the automorphism \(\beta_g\) in the following way:
    • If \(e' \in E\) is a hyperedge, written as \(e' = h.e\), then \(\beta_g(e') = hg.e\)
    • If \(v \in V_i\) is a vertex, and \(v = s_i(e')\), then \(\beta_g(v) = s_i(\beta_g(e'))\).

    We let the reader check that this definition is meaningful. Notice that \(\beta_g(e) = g.e\) and thus \(g_e(\beta_g^{-1}) = g\). Therefore the morphism \(g_e\) is surjective.

Thus \(g_e\) is a group isomorphism between the monodromy group and the automorphism group. Since the monodromy group acts transitively on the set of hyperedges (by connectedness), the dessin is regular. ■

In a regular dessin, the number of hyperedges is equal to the order of the monodromy group or, equivalently, to the order of the automorphism group. Any equality between two of these three integers implies regularity.

regular closure

Consider a connected dessin \(\D = (V_i, E, s_i)\) and denote its monodromy group by \(G\).

Proposition: There exists a regular dessin \(\hat{\D}\) with a morphism to \(\D\), minimal in the following sense: every morphism from a regular dessin to \(\D\) factorizes through \(\hat{\D}\), and unique up to isomorphism. Moreover, the monodromy group (and thus the automorphism group) of \(\hat{\D}\) is isomorphic to \(G\).

This result can be deduced from the existence of the Galois closure for extensions of \(\C(T)\) (using Riemann’s existence theorem to relate these extensions to dessins). However, we give a direct construction:

Proof: First let \(\hat E = G\).

Let \(\hat V_i\) be the set of right classes of \(G\) modulo \(\gen{\sigma_i}\). Every element of \(G\) belongs to exactly one of these right classes: this defines a map \(\hat s_i : \hat E \to \hat V_i\). For each \(v \in \hat V_i\) (which is an orbit in \(G\) under left multiplication by \(\sigma_i\)), a cyclical order on \(\hat s_i^{-1}(v) = v\) is obtained as the order of appearance of elements under repeated multiplication by \(\sigma_i\). We have constructed a dessin \(\hat{\D} = (\hat V_i, \hat E, \hat s_i)\). Notice that the \(i\)-th monodromy element \(\hat\sigma_i\) of the dessin \(\hat{\D}\) is the permutation of \(G\) induced by left multiplication by \(\sigma_i\). Therefore, the monodromy group of \(\hat{\D}\) is isomorphic to \(G\): the embedding \(G \to \Sym_{\hat E} = \Sym_G\) is the left multiplication action. Since the monodromy group has order \(\card{G} = \card{\hat E}\), the dessin \(\hat{\D}\) is regular.

Let us define a morphism of dessins \(\hat{\D} \to \D\). For this, fix an arbitrary hyperedge \(e \in E\). If \(g \in \hat E = G\), let \(\Phi(g) = g.e\). This defines a surjection \(\Phi : \hat E \to E\). If \(v \in \hat V_i\) is a right class of \(G\) modulo \(\gen{\sigma_i}\), then the hyperedges \(g.e\) for \(g \in v\) all have the same image \(\Sigma_i(v)\) under \(s_i\), because \(s_i(\sigma_i.e')=s_i(e')\). For all \(g \in G\), we have \(\Sigma_i(\hat s_i(g)) = s_i(g.e) = s_i(\Phi(g))\). Moreover if \(v \in \hat V_i\) and \(e \in (\hat s_i)^{-1}(v)\), the element following \(e\) in the cyclical order on \((\hat s_i)^{-1}(v)\) is \(\sigma_i e\), and \(\Phi(\sigma_i e) = (\sigma_i e).g = \sigma_i.(e.g) = \sigma_i.\Phi(e)\) is also the element following \(\Phi(e)\) in the cyclical order on \(s_i^{-1}(\Sigma_i(v))\). We have defined a morphism \(\hat D \to D\).

We let the reader check the minimality of \(\hat{\D}\), from which uniqueness follows. ■

faces and clean dessins

Consider a dessin \(\D\), embedded in a compact oriented surface in a way that satisfies the constraints mentioned in the previous post (recall that all these embeddings are equivalent up to a direct homeomorphism of the surface). This situation is always what we mean by an embedded dessin.

Definition (faces): A face of \(\D\) is a connected component of the complement of the embedded dessin.

All faces are homeomorphic to disks.

In what follows, a segment is the part of the boundary of an hyperedge that lies between two adjacent colors: if hyperedges are represented as \(n\)-gons, then segments are the edges of that \(n\)-gon. When \(n=2\), one must still consider that there are two segments: the confusion can be avoided by representing edges as “thick” digons. We see segments as oriented: their orientation respects the order of colors \(1 \to 2 \to \ldots \to n \to 1\) (when \(n=2\), one segment is \(\circ \to \bullet\) and the other one is \(\bullet \to \circ\)). In this way, there is always a hyperedge on the left side of a segment, and a face on the right side of a segment.

Consider a given face and travel along its boundary counterclockwise (i.e. respect the cyclical order on colors \(1 \to 2 \to 3 \to \ldots \to n \to 1 \to \ldots\)). Noting the order in which the segments that make up the boundary of the considered face appear, one obtains a cyclical order on the set of these segments.

Definition (degree of a face): The degree of a face is the number of times that the full order of colors is repeated during a complete travel along the boundary of the face. In other words, one meets in total \(nd\) segments, where \(d\) is the degree of the face.

Faces correspond to cycles in the cycle decomposition of \(\sigma_{n+1}\). The degree of a face is the size of the corresponding cycle. Here is the way this correspondence works: consider a face and travel counterclockwise along its boundary; each time you see a segment of color type \(n \to 1\) (\(\circ \to \bullet\)), record the hyperedge which is on the left side of this segment; the final list of hyperedges is the cycle that corresponds to the chosen face.

Example: Let us consider the \(3\)-dessin \(\D_0\) from the previous blog post. There are two faces. One of them (the outer face) has the following segments on its boundary:

\[r \overset{ (2) }{\to} g \overset{ (1) }{\to} b \overset{ (4) }{\to} r' \overset{ (3) }{\to} g \overset{ (2) }{\to} b' \overset{ (3) }{\to} r' \overset{ (4) }{\to} g' \overset{ (4) }{\to} b \overset{ (1) }{\to} r \to \ldots \text{ (loop)}\]

and so its degree is \(3\). The other one (the inner face) has the following segments on its boundary:

\[r \overset{ (1) }{\to} g \overset{ (3) }{\to} b' \overset{ (2) }{\to} r \to \ldots \text{ (loop)}\]

and so its degree is \(1\).

We deduce from this that \(\sigma_4 = (431)(2)\), by looking at the order of segments of type “blue to red” in these two loops.

clean dessins

Definition (clean dessin): An \(n\)-dessin \(\mathcal{D}\) is clean if its \((n+1)\)-th monodromy element \(\sigma_{n+1}\) is trivial.

From the description of the cycles of \(\sigma_{n+1}\) in terms of the faces of a dessin, one deduces immediately:

Corollary: Consider an embedded dessin \(\D\). The following properties are equivalent:

  • \(\D\) is a clean dessin
  • The ramified cover of \(\P^1(\C)\) corresponding to \(\D\) is unramified at \(t_{n+1}\) (i.e. its actual ramification locus is contained in \(\{t_1, \ldots, t_n\}\))
  • \(\D\) has as many hyperedges as faces
  • All faces of \(\D\) have degree \(1\) (their boundary contains exactly one vertex of each color).

The last property implies that one can swap the roles of hyperedges and faces of a clean dessin. One then obtains another “dual” dessin. This operation corresponds to the interversion of the colors white and yellow in the figure below: since the point \(t_{n+1}\) is not an actual branch point, the complement of the \(n\)-gon is an equally good \(n\)-gon as the original one, except that the cyclical order of the colors is inverted:

Pokéball duality

computing the genus

An dessin \(\D\) embedded on a surface induces a cellular decomposition of that surface:

  • The vertices are the vertices of the dessin. There are \(\sum_i \card{V_i}\) of them.
  • The \(1\)-cells of the decomposition are the segments. There are \(n\card{E}\) of them since each hyperedge of the dessin has \(n\) segments on its boundary.
  • The \(2\)-cells of the decomposition are hyperedges and faces of the dessin. There are \(\kappa + \card{E}\) of them, where \(\kappa\) denotes the number of faces.

We can compute the Euler characteristic of the surface \(S\) on which the dessin is embedded:

\[\chi(S) = \sum_i \card{V_i} + (1-n) \card{E} + \kappa\]

and therefore the genus can be computed too:

\[g(S) = 1 - \frac{1}{2} \left( \sum_i \card{V_i} + (1-n) \card{E} + \kappa \right).\]

In the case of clean dessins, we have \(\kappa = \card{E}\), and therefore the genus in that case is:

\[1 - \frac{1}{2} \left( \sum_i \card{V_i} + (2-n) \card{E} \right).\]

Example: Let us consider the \(3\)-dessin \(\D_0\) from the previous blog post. The genus of the surface on which it is embedded is:

\[1 - \frac{1}{2} \left( 6 + (1-3) \times 4 + 2 \right) = 1.\]

i.e. as we had observed, this dessin is embedded on a torus.

Proposition: The only clean connected dessins d’enfants are of the following form:

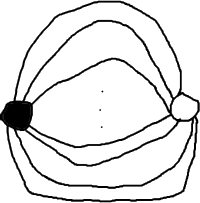
Clean dessins d'enfants

where the number of edges is a positive integer.

Proof: Consider such a dessin d’enfant embedded on a surface \(S\). The genus \(g(S) = 1 - \frac{1}{2} \left( \card{V_{\bullet}} + \card{V_{\circ}} \right)\) is a nonnegative integer, so the dessin has at most \(2\) vertices: one white and one black. The result follows.

cleaning a dessin

Take an \(n\)-dessin. We can convert this dessin into a clean \((n+1)\)-dessin in the following way: add an \((n+1)\)-th color, add one vertex of this new color for each face, and decide that the cyclical order of the hyperedges around one of these new vertices is the order of appearance of the hyperedges corresponding to the segments of color type \(n \to 1\) during a clockwise travel along the boundary of the corresponding face.

In terms of monodromy elements, this is just transforming the \(n\)-tuple \((\sigma_1, \ldots, \sigma_n)\) into the \((n+1)\)-tuple \((\sigma_1, \ldots, \sigma_n, (\sigma_1 \cdots \sigma_n)^{-1})\).

The cleaning process induces an equivalence between the category of \(n\)-dessins and that of clean \((n+1)\)-dessins. Note that cleaning a dessin does not change the genus.

Example: We clean the following dessin d’enfants:

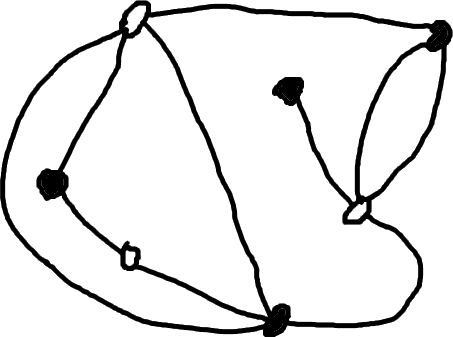
Dessin to clean

It has five faces. We add a vertex of a new color in each face:

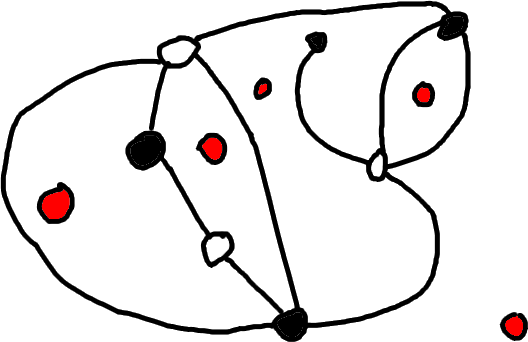
Cleaning half done

We then extend the existing hyperedges by connecting them to new vertices according to the face adjacent to the left side of the edge \(\circ \to \bullet\):

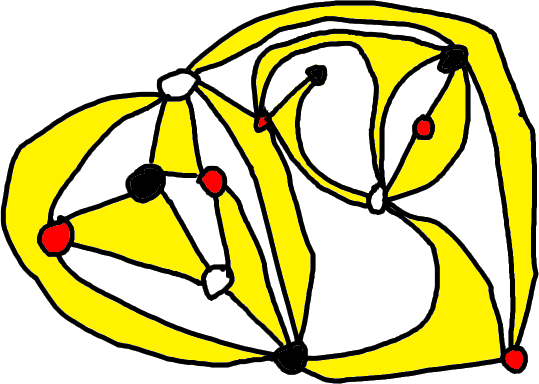
Cleaned dessin

In the next blog post, we will discuss various operations that one can apply to dessins and relate dessins to subgroups of profinite free groups.